SOAL DAN PEMBAHASAN BUKU SISWA MATEMATIKA KLS 9 UJI KOMPETENSI 4 HAL 261 TH 2020
Selesaikan soal-soal berikut ini dengan benar dan sistematis.
1. Perhatikan gambar di bawah ini. Tulislah pasangan bangun yang kongruen.
Pembahasan:
A ≅ K, B ≅ F, C ≅ M, E ≅ H, G ≅ J
2. Perhatikan gambar di bawah.
Jika PQRS kongruen dengan UVRT dan RT = 3/5 RQ,
tentukan panjang PQ.
Pembahasan:
Diketahui :
PQRS kongruen dengan UVRT dan
RT = 3/5 RQ
Ditanyakan :
panjang PQ = ?
Jawab:
RT = PQ = 3/5 RQ
PQ = 3/5 x 8
PQ = 24/5
PQ = 4,8 cm
Jadi panjang PQ adalah 4,8 cm
3. Perhatikan gambar.
Persegi panjang ABCD dibentuk dari 5 persegi panjang
yang kongruen. Jika keliling setiap persegi panjang kecil
adalah 20 cm, maka tentukan keliling dan luas ABCD
Pembahasan:
Perhatikan gambar.
Misal ukuran persegi panjang yang kecil adalah x dan y, maka
Keliling = 20 cm
Keliling = 2(p + l)
2(x + y) = 20
x + y = 20/2
x + y = 10
Perhatikan gambar di atas.
DC = AB
y = x + x + x + x
y = 4x
Substitusikan y = 4x ke persamaan x + y = 10 sehingga
x + y = 10
x + 4x = 10 ( y diganti dengan 4x)
5x = 10
x = 10/5
x = 2
maka,
y = 4x = 4(2) = 8
Jadi,
Panjang = DC = y = 8 cm
Lebar = AD = y + x = 8 + 2 = 10 cm
Keliling ABCD
= 2(p + l)
= 2(8 cm + 10 cm)
= 2(18 cm)
= 36 cm
Luas ABCD
= p × l
= 8 cm × 10 cm
= 80 cm²
4. Diketahui trapesium ABCD dan trapesium FEHG pada
gambar di bawah ini adalah kongruen. Jika panjang AD = 12 cm,
DC = 9 cm, dan EF = 18 cm, tentukan panjang CB.
Pembahasan:
Perhatikan gambar di bawah.
Karena kedua trapesium kongruen maka,
AB = EF = 18 cm ( sisi yang bersesuaian)
Segitiga BCE siku-siku di titik E sehingga berlaku teorema Pythagoras
BC2 = BE2 + CE2
BC2 = 92 + 122
BC2 = 81 + 144
BC2 = 225
BC = √225 = 15 cm
Jadi, panjang CB = BC = 15 cm
5. Pasangan bangun di bawah ini kongruen, tentukan nilai x dan y pada gambar.
(i) x0 + 1280 = 1800 ( sudut dalam sepihak )
x0 = 1800 – 1280
x0 = 520
y0 + 1100 = 1800 ( sudut dalam sepihak )
y0 = 1800 – 1100
x0 = 700
(ii) x0 = 850 sudut yang bersesuaian
y0 + 700 + 1250 + 850 = 3600 (jumlah sudut dalam segiempat)
y0 + 2800 = 3600
y0 = 3600 – 2800
y0 = 800
6. Perhatikan gambar di bawah ini.
Berapa banyak pasangan segitiga kongruen pada setiap bangun di atas?
Tuliskan semua pasangan segitiga kongruen tersebut.
Pembahasan:
Semua pasangan segitiga kongruen yaitu:
a. ada 3 pasang, yaitu ΔAED ≅ ΔAEB, ΔCDE ≅ ΔCBE, ΔADC ≅ ΔABC
b. ada 4 pasang, yaitu ΔIFJ ≅ ΔGHI, ΔFIH ≅ ΔHGF, ΔIJH ≅ ΔGJF,
ΔIJF ≅ ΔGJH
c. ada 2 pasang, yaitu ΔMKO ≅ ΔNLO, ΔMKL ≅ ΔNLK
d. ada 3 pasang, yaitu ΔPST ≅ ΔQRT, ΔPSR ≅ ΔQRS, ΔPSQ ≅ ΔQRP
7. Apakah pasangan segitiga berikut ini pasti kongruen? Jika ya, kriteria apakah
yang menjamin pasangan segitiga berikut ini kongruen?
Pembahasan:
a. Iya, dijamin kongruen dengan kriteria sisi – sudut –sisi
b. Iya, dijamin kongruen dengan kriteria sudut 90o –sisi miring – satu sisi
siku (kekongruenan khusus segitiga siku-siku)
c. Iya, dijamin kongruen dengan kriteria sudut – sisi –sudut
d. Iya, dijamin kongruen dengan kriteria sudut – sisi –sudut atau kriteria sisi
–sudut – sudut
e. Iya, dijamin kongruen dengan kriteria sisi – sudut –sisi
8. Tuliskan satu pasangan segitiga kongruen pada setiap bangun berikut dan tunjukkan.
Pembahasan:
a. Contoh: ΔPQN ≅ ΔPRM
Bukti: PN = PM (diketahui)
m∠QPN = m∠RPM (berhimpit)
PQ = PR (diketahui)
Jadi, ΔPQN ≅ ΔPRM (berdasarkan kriteria sisi – sudut –sisi)
(pasangan segitiga kongruen yang lain silakan dicari dan dibuktikan)
b. ΔPSR ≅ ΔQXP
Bukti: SR = PX (diketahui)
m∠PRS = m∠QPX (berseberangan dalam, karena SR//PQ)
PR = QP (ΔPQR segitiga samasisi)
Jadi, ΔPSR ≅ ΔQXP (berdasarkan kriteria sisi – sudut –sisi)
c. Contoh: ΔABC ≅ ΔCDA
AB//DC, AD//BC akibatnya AB = CD dan AD = CB
AC (pada ΔABC) = AC (pada ΔCDA)
Jadi, ΔABC ≅ ΔCDA (berdasarkan kriteria sisi – sisi –sisi)
Pembuktian ΔABC ≅ ΔCDA juga bisa dengan kriteria sudut –sisi – sudut
m∠BAC = m∠DCA (berseberangan dalam, karena AB//DC)
AC (pada ΔABC) = AC (pada ΔCDA) (berhimpit)
m∠ACB = m∠CAD (berseberangan dalam, karena AB//DC)
Jadi, ΔABC ≅ ΔCDA (berdasarkan kriteria sudut – sisi –sudut)
(pasangan segitiga kongruen yang lain silakan dicari dan dibuktikan)
9. Perhatikan gambar.
Diketahui ∆PQR ≅ ∆LKM dan m∠PQR = 60o.
Tentukanlah:
a. besar m∠PRQ
b. besar m∠LKM
c. besar m∠KML
d. panjang KL
e. Panjang KM
Pembahasan:
a. ∠PRQ = 1800 – (∠QPR + ∠PQR)
∠PRQ = 1800 – (900+ 600)
∠PRQ = 1800 – 1500
∠PRQ = 300
b. ∠LKM = ∠PQR = 600 sudut yang bersesuaian
c. ∠KML = ∠PRQ = 300 sudut yang bersesuaian
d. Perhatikan ΔPRQ siku-siku di titik P maka berlaku rumus Pythagoras
PQ2= QR2 – PR2
PQ2= 132 – 122
PQ2= 169 – 144
PQ2 = 25
PQ = √25
PQ = 5 cm
Jadi panjang KL = PQ = 5 cm
e. KM = QR = 13 cm sisi yang bersesuaian
10. Perhatikan gambar di bawah.
Diketahui AC = AE dan m∠BAC = m∠DAE
a. Tunjukkan bahwa ∆ABC ≅ ∆ADE.
b. Jika CD = 2 cm dan AE = 10 cm,
tentukanlah panjang BC dan AB
Pembahasan:
a. AC = AE (diketahui)
m∠BAC = m∠DAE (diketahui)
m∠ABC = m∠ADE (diketahui siku-siku)
Jadi, ΔABC ≅ ΔADE berdasarkan kriteria sisi – sudut –sudut
b. Perhatikan gambar di bawah
AB = AC – CD
AB = 10 – 2 = 8 cm
Jadi panjang AB adalah 8 cm
BC² = AC² – AB²
BC² = 10² – 8²
BC² = 100 – 64
BC² = 36
BC = √36
BC = 6 cm
Jadi panjang BC adalah 6 cm
11. Perhatikan gambar di bawah.
Diketahui panjang AB = 13 cm dan EF = 5 cm.
a. Buktikan bahwa ∆AFE ≅ ∆DFE
b. Buktikan bahwa ∆DCB ≅ ∆DFE
c. Hitunglah panjang AC
d. Hitunglah panjang AE
Pembahasan:
a. AF = DF (diketahui)
m∠AFE = m∠DFE = 90o (diketahui siku-siku)
EF (pada ΔAFE) = EF (pada ΔDFE) (berhimpit)
Jadi, ΔAFE ≅ ΔDFE berdasarkan kriteria sisi – sudut –sisi.
b. DC = DF (diketahui)
m∠BDC = m∠EDF (bertolak belakang)
DB = DE (diketahui)
Jadi, ΔDCB ≅ ΔDFE berdasarkan kriteria sisi – sudut –sisi.
c. EF = 5 cm, BC = EF = 5 cm
(karena ΔDCB ≅ ΔDFE dan BC bersesuaian dengan EF )
AB = 13 cm, BC = 5 cm, ΔABC siku-siku di C, dengan teorema Phytagoras:
AC2 = AB2 – BC2
AC2 = 132 – 52
AC2 = 169 – 25
AC2 = 144
AC = √144
maka AC = 12 cm.
d. Lihat ΔAFE, EF = 5 cm, AF = AC/3 = 12/3 = 4 cm,
dengan teorema Phytagoras maka
AE2 = EF2 + AF2
AE2 = 52 + 42
AE2 = 25 + 16
AE2 = 41
AE = √41
maka AE = √41 cm.
12. Apakah bangun di bawah ini pasti sebangun? Jelaskan.
a. dua persegi c. dua segitiga sama sisi
b. dua lingkaran d. dua belah ketupat
Pembahasan:
a. dua persegi → pasti sebangun
b. dua lingkaran → pasti sebangun
c. dua segitiga sama sisi → pasti sebangun
d. dua belah ketupat → belum tentu sebangun
13. Trapesium ABCD sebangun dengan trapesium RSPQ, tentukan
nilai x dan y pada gambar di bawah.
Mencari x
CD : PQ = AB : RS
x : 21 = 10 : 15
x × 15 = 10 × 21
x × 15 = 210
x = 210/15
x = 14 cm
Mencari y
QR : AD = RS : AB
y : 12 = 15 : 10
y × 10 = 15 × 12
y × 10 = 180
y = 180/10
y = 18 cm
14. Perhatikan gambar berikut ini.
a. Jika trapesium (i) dan (ii) sebangun, tentukan nilai p, q, r dan s.
b. Tentukan perbandingan keliling trapesium (i) dan (ii).
c. Tentukan perbandingan luas trapesium (i) dan (ii).
Pembahasan:
a. Mencari p
p : 12 = 12 : 8
p × 8 = 12 × 12
p × 8 = 144
p = 144/8
p = 18 cm
Mencari q
q : 27 = 8 : 12
q × 12 = 8 × 27
q × 12 = 216
q = 216/12
q = 18 cm
Mencari r perhatikan gambar di bawah:
Dari gambar di peroleh
a = q – 12
a = 18 – 12
a = 6 cm
Sehingga,
r2 = 82 + a2
r2 = 82 + 62
r2 = 64 + 36
r2 = 100
r = √100
r = 10 cm
Mencari s
s : r = 12 : 8
s : 10 = 12 : 8
s × 8 = 12 × 10
s × 8 = 120
s = 120/8
s = 15 cm
b. Perbandingan keliling trapesium (i) dan (ii)
= keliling trapesium (i) : keliling trapesium (ii)
= (12 + 8 + 18 + 10) : (27 + 12 + 18 + 15)
= 48 : 72
= 2 : 3
c. Perbandingan luas trapesium (i) dan (ii)
= luas trapesium (i) : luas trapesium (ii)
= (1/2 (12 + 18)8) : (1/2 (27 + 18)12)
= (1/2 (30)8) : (1/2 (45)12)
= 120 : 270
= 4 : 9
15. Hitunglah panjang sisi yang ditanyakan pada gambar berikut ini.
Pembahasan:
a. EF : AB = CF : CB
EF : 8 = 6 : (6+4)
EF : 8 = 6 : 10
EF × 10 = 6 × 8
EF × 10 = 48
EF = 48/10
EF = 4,8 cm
b. AB : EF = CB : CF
AB : 6 = 7 : 4
AB × 4 = 7 × 6
AB × 4 = 42
AB = 42/4
AB = 10,5 cm
c. CA : CE = AB : EF
9 : (9 – AE) = 6 : 2
6 × (9 – AE) = 9 × 2
54 – 6AE = 18
54 – 18 = 6AE
36 = 6AE
AE = 36/6
AE = 6 cm
d. CF : CB = EF : AB
CF : (CF + 4) = 5 : 7
CF × 7 = 5 × (CF + 4)
7CF = 5CF + 20
7CF – 5CF = 20
2CF = 20
CF = 20/2
CF = 10 cm
e. AE : BD = CE : BC
AE : 6 = 14 : 7
7AE = 6 × 14
7AE = 84
AE = 84/7
AE = 12 cm
f. Perhatikan gambar
EG : BH = CG : CH
EG : 6 = 6 : 9
EG × 9 = 6 × 6
EG × 9 = 36
EG = 36/9
EG = 4 cm
Jadi panjang EF = EG + EF = 4 + 2 = 6 cm
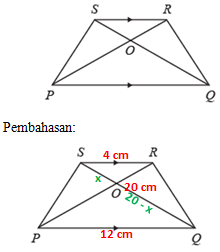
16. Diketahui trapesium sama kaki PQRS pada gambar di bawah ini,
dengan panjang SR = 4 cm, PQ = 12 cm, dan QS = 20 cm.
Tentukan panjang SO.
Diketahui :
Trapesium PQRS di atas
SR = 4 cm
PQ = 12 cm
SQ = 20 cm
Ditanyakan : Panjang SO ?
Jawab :
Misal panjang SO = x
Maka OQ = SQ – SO = 20 – x
Kita masukkan pada sisi-sisi yang bersesuaian.
PQ : SR = OQ : SO
12 : 4 = (20 – x) : x
3 : 1 = (20 – x) : x
3x = 1 (20 – x)
3x = 20 – x
3x + x = 20
4x = 20
x = 20/4
x = 5
Jadi panjang SO adalah 5 cm
17. Perhatikan gambar.
a. Tuliskan pasangan segitiga sebangun pada gambar tersebut.
b. Dari tiap-tiap pasangan segitiga sebangun tersebut,tentukan pasangan sisi yang
bersesuaian dan buat perbandingannya.
c. Tentukan panjang NK, KL, dan MK.
Pembatasan:
a. Pasangan segitiga sebangun yaitu
ΔMKL ∼ΔMNK, ΔMKL ∼ ΔKNL, dan ΔMNK ∼ΔNKL
b. Pasangan sisi yang bersesuaian dan buat perbandingannya
ΔMKL ∼ΔMNK, perbandingan sisi yang bersesuaian yaitu
MK/MN = KL/NK = LM/LK
ΔMKL ∼ΔKNL, perbandingan sisi yang bersesuaian yaitu
MK/KN = KL/NL = LM/LK
ΔMNK ∼ΔNKL, perbandingan sisi yang bersesuaian yaitu
MN/NK = KN/KL = MK/NL
c. NK² = LN × NM
NK² = 9 × 16
NK² = 144
NK = √144
NK = 12 cm
KL² = LN × LM
KL² = 9 × (9 + 16)
KL² = 9 × 25
KL = √9 × √25
KL = 3 × 5
KL = 15 cm
MK² = NM × LM
MK² = 16 × 25
MK = √16 × √25
MK = 4 × 5
MK = 20 cm
18. ABCD adalah persegi.
Jika DE = CF, maka tentukanlah panjang:
a. DE d. OC
b. OE e. OF
c. OD
Pembahasan:
Diketahui:
ABCD persegi
DE = CF
DA = DC = AB = CB = 8 cm
EB = 2 cm
CE = CB – EB = 8 – 2 = 6 cm
Untuk mencari sisi miring dari segitiga, gunakan pythagoras.
DE² = DC² + CE²
DE² = 8² + 6²
DE² = 64 + 36
DE² = 100
DE = √100
DE = 10 cm
CF = 10 cm
Karena DE = CF dan keduanya berpotongan (segitiga DCE dan CBF kongruen),
maka sudut COE 900.
DC x CE = OC x DE
8 x 6 = OC x 10
48 = OC × 10
OC = 48/10
OC = 4,8 cm
OF = CF – CO
OF = 10 – 4,8
OF = 5,2 cm
DO² = DC² – CO²
DO² = 8² – 4,8²
DO² = 64 – 32,04
DO² = 22,40
DO = 4,7 cm
OE = DE – DO
OE = 10 – 4,7
OE = 5,3 cm
19. Hitunglah panjang sisi yang diberi label pada gambar di bawah ini.
(semua dalam satuan sentimeter)
Pembahasan:
Gambar 1
PQ = 15
PT = 9
TR = 12
QR = 30
PR = PT + TR = 9 + 12 = 21
PST//PQR
a/PQ = PT/PR
a/15 = 9/21
a = 9×15/21
a = 6,43
b/PT = QR/PR
b/9 = 30/21
b = 30×9/21
b = 12,86
Gambar 2
Perhatikan segitiga KQM dan segitiga LQR adalah
dua segitiga sebangun, sehingga:
QM : QR = KM : LR = KQ : LQ
↔ d : 5 = 12 : f = 14 : e
Perhatikan segitiga MQP dan segitiga MRL adalah
dua segitiga sebangun, sehingga:
MQ : MR = MP : ML = PQ : LR
↔ d : (d + 5) = 7 + (c + 7) = 5 : f
Dari perbandingan di atas kita peroleh:
d : 5 = 12 : f
↔ df = 60
d : (d + 5) = 5 : f
↔ df = 5d + 25
Akibatnya:
5d + 25 = 60
↔ 5d = 35
↔ d = 7
df = 60
↔ 7f = 60
↔ f = 60/7
7 + (c + 7) = 5 : f
↔ 5c + 35 = 7f
↔ 5c = 7(60/7) – 35
↔ 5c = 60 – 35
↔ c = 25/5 = 5
12 : f = 14 : e
↔ 12e = 14f
↔ 12e = 14(60/7)
↔ 12e = 120
↔ e = 10
Jadi, c = 5, d = 7, e = 10, dan f = 60/7 = 8 4/7
Gambar 3:
EF : AB = CF : CB
6 : 9 = 8 : (8 + p)
6(8 + p) = 9 × 8
48 + 6p = 72
6p = 72 – 48
6p = 24
p = 24/6 = 4
FB : BC = FG : CD
4 : 12 = q : 24
12q = 4 × 24
12q = 96
q = 96/12 = 8
Gambar 4:
SO : RO = TO : QO
10 : 18 = 14 : x
10x = 18 × 14
10x = 252
x = 252/10 = 25,2
ST : QR = SO : RO
16 : y = 10 : 18
10y = 16 × 18
10y = 288
y = 288/10 = 28,8
ST : QR = PS : PQ
16 : 28,8 = 12 : (12 + z)
16(12 + z) = 28,8 × 12
192 + 16z = 345,6
16z = 345,6 – 192
16z = 153,6
z = 153,6/16 = 9,6
20. Dua belas tusuk gigi disusun seperti pada gambar di samping.
Dengan memindahkan hanya dua tusuk gigi bagaimana kamu
membentuk enam persegi atau tujuh persegi?
Gambar di atas bisa dikatakan terdiri atas 6 persegi yaitu 2 persegi besar dan
4 persegi kecil. Dapat juga dikatakan terdiri atas 7 persegi yaitu 3 persegi besar
dan 4 persegi kecil.
21. Enam belas tusuk gigi disusun seperti gambar di samping.
Dengan memindahkan hanya dua tusuk gigi bagaimana
kamu membentuk empat persegi?
22. Pada gambar di bawah ini menunjukkan persegi yang dibentuk
dengan 20 tusuk gigi. Di tengahnya terdapat lubang kotak dengan
luas 1/25 luas seluruhnya. Dengan menggunakan 18 tusuk gigi, bagilah
luasan di antara persegi luar dan persegi di tengah menjadi 6 daerah
yang sebangun.
23. Perhatikan gambar.
Bangun PINK, NOTE, dan BLUE adalah persegi. Panjang
KN = 5 cm dan NE = 9 cm, Titik P –O –B terletak dalam satu
garis lurus. Tentukan panjang sisi dan luas bangun BLUE.
Pembahasan:
Diketahui
Persegi PINK ⇒ KN = 5 cm
Persegi NOTE ⇒ NE = 9 cm
Pegitga OPI ⇒ PI = KN = 5 cm
OI = NO – NI
OI = 9 – 5 = 4 cm
Pegitiga BOT ⇒ OT = 9 cm
Kita akan menggunakan dua segitiga sebangun untuk mencari panjang BT agar
selanjutnya bisa menentukan panjang sisi BE.
Sisi-sisi yg bersesuaian mempunyai perbandingan yg sama pada Δ OPI dan Δ BOT.
PI / OT = OI / BT = PO / OB
PI / OT = OI / BT
5 / 9 = 4 / BT
5 BT = 4 × 9
5 BT = 36
BT = 36 / 5
BT = 7,2 cm
Panjang BE = BT + TE
= 7,2 cm + 9 cm
= 16,2 cm
Luas persegi BLUE = 16,2 cm × 16,2 cm
= 262,44 cm²
Jadi luas bangun BLUE adalah 262,44 cm²
24. Pada gambar di bawah ini, tinggi tongkat PQ sesungguhnya adalah 4 m
dan panjang bayangannya 15 m. Jika panjang bayangan pohon adalah
30 m, tentukan tinggi pohon.
Pembahasan:
Diketahui :
Tinggi tongkat PQ = 4 m
Panjang bayangan tongkat OQ = 15 m
Panjang bayangan pohon OR = 30 m
Ditanya :
Tinggi pohon SR ?
Jawab :
Δ QOP sebangun dengan Δ ROS
Sisi-sisi yg bersesuaian
OQ dengan OR
PQ dengan RS
Menentukan tinggi pohon
OQ/OR = PQ/SR
15/30 = 4/SR
15 SR = 30 × 4
15 SR = 120
SR = 120/15
SR = 8
Jadi tinggi pohon tersebut adalah 8 m
25. Sekelompok peserta jelajah alam mendapat tugas untuk menaksir lebar suatu
sungai tanpa mengukurnya secara langsung. Mereka menentukan titik acuan
di seberang sungai yaitu titik A. Satu peserta lain berdiri di titik C.
Peserta yang lain berdiri di titik B tepat di depan A. Kemudian berjalan menuju
ke titik F dengan jarak B ke F adalah dua kali jarak B ke C. Dari titik F ia berjalan
menuju titik D, di mana dengan pandangannya objek di titik A-C-D terletak pada
satu garis lurus. Sehingga lebar sungai dapat diketahui dengan mengukur jarak F ke D.
Apakah cara tersebut tepat utuk menaksir lebar sungai? Jelaskan.
Pembahasan:
Iya, tentu. Cara tersebut menggunakan konsep kekongruenan dua segitiga
dalam gambar di atas yaitu ΔABC dan ΔDFC. Silakan dibuktikan.
Petunjuk: gunakan kriteria kekongruenan sudut-sisi-sudut
(gunakan titik sudut B, C, dan F dan sisi BC dan FC)



