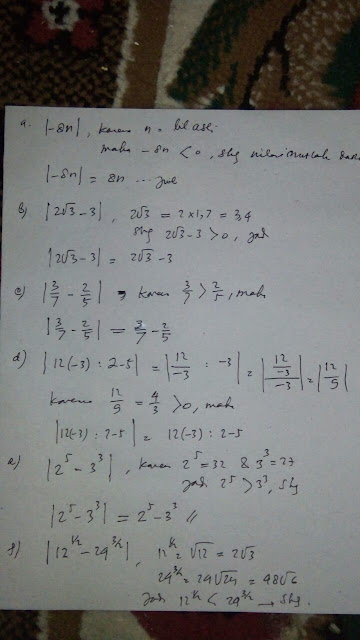Kunci Jawaban Uji Kompetensi 1.1 Matematika SMA Kelas 10 Hal 25

2. Manakah pernyataan berikut ini yang merupakan pernyataan bernilai benar? Berikan alasanmu.
a. |k| = k , untuk setiap k bilangan asli
b. |x| = x , untuk setiap bilangan bulat
c. Jika |x| = -2 , maka x = -2 .
d. Jika 2t – 2 > 0 , maka |2t-2| = 2t – 2
e. Jika |x + a| = b , dengan a,b,x bilangan real, maka nilai x yang memenuhi hanya x = b-a

|k| = k , untuk setiap k bilangan asli

→ Oleh karena himpunan bilangan asli adalah {1, 2, 3, …} dimana setiap elemennya > 0, maka pernyataan bernilai benar.

|x| = x , untuk setiap bilangan bulat

→ Oleh karena himpunan bilangan bulat adalah { …, -2 , -1 , 0, 1, 2, … } maka pernyataan tidak benar untuk x < 0.

Jika |x| = -2 , maka x = -2.

→ Oleh karena |x| ≥ 0, maka soal sudah salah. Dengan demikian, pernyataannya pun salah.

Jika 2t – 2 > 0 , maka |2t – 2| = 2t – 2.

→ Pernyataan bernilai benar karena sesuai dengan definisi nilai mutlak.

Jika |x + a| = b, dengan a, b, x bilangan real, maka nilai x yang memenuhi hanya x = b – a.

→ jika x + a ≥ 0 maka x + a = b atau x = b – a

→ jika x + a < 0, maka x + a = -b atau x = -b – a

→ berdasarkan uraian di atas, pernyataan bernilai salah

A. Benar, sebab bilangan asli bernilai positif.

B. Salah, sebab untuk x < 0, |x| = -x.

C. Pernyataan salah, sebab |x| selalu positif.

D. Salah, sebab untuk x + a < 0 atau x < -a, |x+a| = -(x+a) = -x – a, sehingga

     -x – a = b atau -x = b + a atau x = -b – a.

E. Benar, karena berdasarkan definisinya, nilai mutlak sebarang bilangan merupakan bilangan positif.

f. salah karena x=0 memenuhi

g. benar cek definisi nilai mutlak

3. Hitunglah nilai x (jika ada) yang memenuhi persamaan nilai mutlak berikut. jika tidak ada nilai x yang memenuhi, berikan alasanmu

a) |4-3x| = |-4|
b) 2|3x-8| = 10
c) 2x+ |3x-8| = -4
d) 5 |2x-3| = 2|3-5x|
e) 2x+ |8-3x| = |x-4|

|4 – 3x| = |-4|

|4 – 3x| = 4

4 – 3x = 4

4 – 4 = 3x

3x = 0

x = 0

4 – 3x = -4

3x = 4 + 4

3x = 8

x = 8/3

Hp : {0 , 8/3}

————————————————

2|3x – 8| = 10

|3x – 8| = 5

3x – 8 = 5

3x = 13

x = 13/3

3x – 8 = -5

3x = 3

x = 1

Hp : {1 , 13/3}

————————————————

2x + |8 – 3x| = |x – 4|

|x – 4| – |8 – 3x| = 2x

x – 4 – 8 + 3x = 2x

4x – 12 = 2x

4x – 2x = 12

2x = 12

x = 6

x – 4 – 8 + 3x = -2x

4x – 12 = -2x

4x + 2x = 12

6x = 12

x = 2

Hp : {2 , 6}

————————————————

5|2x – 3| = 2|3 – 5x|

(10x – 15)² = (6 – 10x)²

(10x – 15)² – (6 – 10x)² = 0

(10x – 15 + 6 – 10x)(10x – 15 – 6 + 10x) = 0

(-9)(20x – 21) = 0

-180x + 189 = 0

180x = 189

x = 189/180

x = 21/20

Hp = {21/20}

————————————————

2x + |3x – 8| = -4

|3x – 8| -4 – 2x

(3x – 8)² = (-4 – 2x)²

(3x – 8)² – (-4 – 2x)² = 0

(x – 12)(5x – 4) = 0

x = 4/5

x = 12

Hp : {4/5 , 12}

4. Suatu grup musik merilis album, penjualan per minggu (dalam ribuan) dinyatakan dengan model s (t) = -2|t-22| + 44, t waktu (dalam minggu)

a) gambark grafik fungsi penjualan s (t)
b) hitunglah total penjualan album selama 44 minggu pertama
c) dinyatakan album emas jika penjualan lebih dari 500.000 copy. Hitunglah t agar dinyatakan album emas ,tolong bantuannya

5. Selesaikan setiap persamaan nilai mutlak berikut ini.
A) |2y+5|=|7-2y|
B) |x-1|+|2x|+|3x+1|=6
C) |4x-3|=-|2x-1|
D) |3p+2|/4 = |1/2p-2|
E) -|3-6y| = |8-2y|
F) |3,5x – 1,2| = |8,5x + 6|

a) |2y + 5| = |7 – 2y|

(2y + 5)² = (7 – 2y)²

4y² + 20y + 25 = 49 – 28y + 4y²

20y + 25 = 49 – 28y

48y = 24

y = 24/48

y = 1/2

b). |x – 1| + |2x| + |3x + 1| = 6

(i)

x – 1 + 2x + 3x + 1 = 6

6x = 6

x = 1

(ii)

x – 1 + 2x + 3x + 1 = -6

6x = -6

x = -1

jadi HP : {-1 , 1}

c) |4x – 3| = -|2x – 1|

nilai mutlak = -(sesuatu)

maka tidak ada nilai yang memenuhi

HP : { }

d.)  juga sama. tidak ada nilai x yang memenuhi

HP : { }

e.) |3,5x – 1,2| = |8,5x + 6|

(3,5x – 1,2)² = (8,5x + 6)²

12,25x² – 8,4x + 1,44 = 72,25x² + 102x + 36

60x² + 110,4x + 34,56 = 0

x² + 1,84x + 0,576 = 0

x = -1.44

atau

x = -0,4

f. 3,5x-1,2=8,5x+6
3,5x-8,5x=6+1,2
-5x = 7,2
x = 7,2/-5
x = -1,44
atau
3,5x-1,2 = -(8,5x+6)
3,5x-1,2 = -8,5x – 6
3,5x+8,5x = -6+1,2
12x = -4,8
x = -4,8/12
x = -0,4
x= { -1,44 , -0,4 }

6. Selidiki kebenaran setiap pernyataan berikut ini dan berikan alasan untuk setiap pernyataanmu a) untuk setiap x,y bilangan real, |xy| = |x| . |y|

SAYA GANTI HURUH X DAN Y MENJADI ANGKA 2 DAN 8

|xy| = |x| . |y|

= |2.8| = |2| . |8|

= | 16 | = |2.8|

= 16 = 16

PENJELASANNYA BAHWA PENYATAANB TERSEBUT BENAR DAN MERUPAKAN SIFAT-SIFAT NILAI MUTLAK UNTUK SEMBARANG YANG BILANGAN x DAN y bilangan real