Tak Berkategori

Kunci Jawaban Buku Matematika Kelas 10 Kurikulum 2013 Uji Kompetensi 1.2

April 29, 2019
402
Views

Kunci Jawaban Buku Matematika Kelas 10 Kurikulum 2013 Uji Kompetensi 1.2

1. Manakah dari pernyataan di bawah ini yang benar?Berikan alasanmu.
a) untuk setiap x bilangan real,berlaku bahwa |x| lebih dari sama dengan 0.
b)tidak terdapat bilangan real x,sehingga |x| < -8.
c)|n| lebih dari sama dengan |m|,untuk setiap n bilangan asli dan m bilangan bulat.
Pembahasan :
A benar karena karena nilai mutlak itu pasti lebih dari atau sama dengan nol
b benar, karena nilai mutlak selalu positif tidak mungkin kurang dari negatif
c salah, karena ada bilangan asli n=1 dan bilangan bulat m=2 tetapi n<m
2. Selesaikan pertidaksamaan nilai mutlak berikut !!

(a) [ 3 – 2x ]<4

(b) [ x/2 + 5 ]> 9

(c) [ 3x + 2 ]< 5

(d) 2< [ 2 – x/2 ]< 3 

Pembahasan :
|3 – 2x| < 4
(3 – 2x)² < 4²
(3 – 2x)² – 4² < 0
ingat bahwa :
a² – b² = (a + b)(a – b)
sehingga :
(3 – 2x + 4)(3 – 2x – 4) < 0
(-2x + 7)(-2x – 1) < 0
-2x + 7 = 0
-2x = -7
2x = 7
x = 7/2
-2x – 1 = 0
-2x = 1
2x = -1
x = -1/2
uji nilai x di titik 0
(0 + 7)(0 – 1) < 0
(7)(-1) < 0
-7 < 0
memenuhi
karena 0 berada di antara -1/2 dan 7/2, dan 0 memenuhi pertidaksamaan, maka :
HP = {x | -1/2 < x < 7/2, x∈R}
==========
|x/2 + 5| > 9
(x/2 + 5)² > 9²
(x/2 + 5)² – 9² > 0
(x/2 + 5 + 9)(x/2 + 5 – 9) > 0
(x/2 + 14)(x/2 – 4) > 0
x/2 + 14 = 0
x/2 = -14
x = -28
x/2 -4 = 0
x/2 = 4
x = 8
uji nilai 0 pada x
(0 + 14)(0 – 4) > 0
(14)(-4) > 0
-56 > 0
tidak memenuhi
karena 0 berada di antara 8 dan -28, namun 0 tidak memenuhi persyaratan, maka :
HP = {x | x < -28 atau x > 8, x∈R}
==========
|3x + 2| < 5
(3x + 2)² < 5²
(3x + 2)² – 5² < 0
(3x + 2 + 5)(3x + 2 – 5) < 0
(3x + 7)(3x – 3) < 0
3x + 7 = 0
3x = -7
x = -7/3
3x – 3 = 0
3x = 3
x = 1
uji nilai 0 pada x
(0 + 7)(0 – 3) < 0
(7)(-3) < 0
-21 < 0
memenuhi
0 berada di antara -7/3 dan 1, sehingga :
HP = {x | -7/3 < x < 1, x∈R}
==========
2 < |2 – x/2| < 3
partisi pertidaksamaan
2 < |2 – x/2|
atau
|2 – x/2| > 2
(2 – x/2)² > 2²
(2 – x/2)² – 2² > 0
(2 – x/2 + 2)(2 – x/2 – 2) > 0
(-x/2 + 4)(x/2) > 0
-x/2 + 4 = 0
-x/2 = -4
x/2 = 4
x = 8
x/2 = 0
x = 0
uji nilai 2 pada x
(-2/2 + 4)(2/2) > 0
(-1+4)(1) > 0
(3)(1) > 0
3 > 0
memenuhi
2 berada di antara 0 dan 8, dan 2 memenuhi syarat, sehingga :
HP1 = (0, 8)
|2 – x/2| < 3
(2 – x/2)² < 3²
(2 – x/2)² – 3² < 0
(2 – x/2 + 3)(2 – x/2 – 3) < 0
(-x/2 + 5)(-x/2 – 1) < 0
-x/2 + 5 = 0
-x/2 = -5
x/2 = 5
x = 10
-x/2 – 1 = 0
-x/2 = 1
x/2 = -1
x = -2
uji nilai 0 pada x
(5)(-1) < 0
-5 < 0
memenuhi
0 berada di antara -2 dan 10, dan 0 memenuhi pertidaksamaan, sehingga :
HP2 = (-2, 10)
HP total = HP1 n HP2
= (0, 8) n (-2, 10)
= (0, 8)
HP = {x | 0 < x < 8, x∈R}
3. Maria memiliki nilai ujian matematika : 79, 67, 83, dan 90. Jika dia harus ujian sekali lagi dan berharap mempunyai nilai rata-rata 81, berapa nilai yang harus dia raih sehingga nilai rata-rata yang diperoleh paling rendah menyimpang 2 poin?
Pembahasan :
Rata-rata= total data/jumlah data
misal nilai yang diinginkan adalah x
81= 79+67+83+90+x/5
81 x 5 = 79+67+83+90+x
405 = 319+x
x= 405-319
x= 86
ia harus mendapat nilai 86 jika ingin rata-ratanya 81
jika menyimpang 2 poin berarti 79. caranya sama
79= 79+67+83+90+x/5
395= 319+x
x= 395-319
x= 76
4. Sketsa grafik y=[3x-2]-1, untuk -2<5 dan X bilangan real?
Pembahasan :
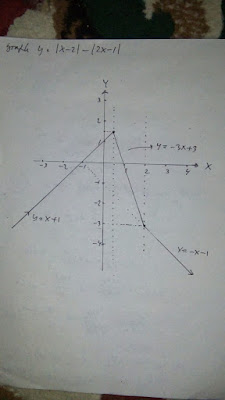
5. Sketsa grafik y=|x-2|-|2x-1|,untuk x bilangan real
Pembahasan :
6. Hitung semua nilai x yang memenuhi kondisi berikut ini.
a). Semua bilangan real yang jaraknya ke nol adalah 10
b). Semua bilangan real yang jaraknya dari 4 adalah kurang dari 6
Pembahasan :
A) | x | = 10
x = 10  atau x =-10
b) |x -4| < 6
-6 < x – 4 < 6
-2 < x < 10
x = -1,0,1,2,3,4,5,6,7,8,9
7. Level hemoglobin normal pada darah laki laki dewasa adalah antara 13 dan 16 gram per desiliter (g/dL)

a) Nyatakan dalam suatu pertidaksamaan nilai mutlak yang merepresentasikan level hemoglobin normal untuk laki-laki dewasa.

b) Tentukan level hemoglobin yang merepresentasikan level hemoglobin tidak normal untuk laki-laki dewasa.

Pembahasan :
Misalkan hemoglobin pada darah adalah h
a) Hemoglobin normal adalah antara 13 dan 16 maka kalau dinyatakan dalam pertidaksamaan adalah :
13 < h < 16
Dalam pertidaksamaan nilai mutlak ditulis : |h – 14,5| < 1,5
Sebab jika dihitung akan memenuhi 13 < h < 16
b) Hemoglobin tidak normal adalah
h >= (lebih dari sama dengan) 16 atau h <= (kurang dari sama dengan) 13 sehingga dalam pertidaksamaan nilai mutlak ditulis :
|t – 14,5| >= (lebih dari sama dengan) 1,5
8. Berdasarkan definisi atau sifat, buktikan |a-b| lebih kecil sama dengan |a+b|
Pembahasan :
|a-b| akan selalu <= |a+b| hanya bila a dan b positif. penambahan berarti jumlahnya makin banyak, sedangkan pengurangan sebaliknya
9. Gambarkan himpunan penyelesaian PERTIDAKSAMAAN LINEAR berikut ini dengan memanfaatkan garis bilangan
A.)4< I x-1 I + I x-1 I<5
B.)I x-2 I< Ix-1 I
c.)IxI + I x+1 I<2
Pembahasan :
10. Diketahui fungsi f(x)=5-2x, 2 lebih kecil sama dengan x lebih kecil sama dengan 6. tentukan nilai m sehingga |f(x)| lebih kecil sama dengan m. hitunglah p untuk |f(x)|lebih kecil sama dengan p
Pembahasan :
f(x) = 5 – 2x, 2≤ x ≤ 6
Karena f(x) monoton turun, maka uji x pada ujung domain.
|f(2)| = |5 – 2(2)| = |5 – 4| = 1
f(6) = |5 – 2(6)| = |5 – 12| = 7
Jadi, pilih m = 7, sehingga |f(x)| ≤ m
Bisa juga pilih m lebih besar dari 7, yang penting nilai m tidak kurang dari tujuh.
Hal yang sama dapat dikerjakan untuk mencari p.