Jawaban Buku Paket Matematika SMA Kelas 10 Uji Kompetensi 3.2 Fungsi

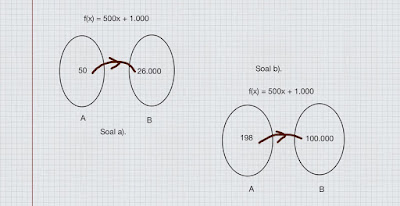
1. Seorang pedagang kain memperoleh keuntungan dari hasil penjualan setiap x potong kain sebesar f(x) rupiah. nilai keuntungan yang diperoleh mengikuti fungsi f(x) = 500x + 1.000, (dalam ribuan rupiah) x adalah banyak potong kain yang terjual.
a) Jika dalam suatu hari pedagang tersebut mampu menjual 50 potong kain, berapa keuntungan yang diperoleh ?
b) jika keuntungan yang diharapkan sebesar Rp100.000,00 berapa potong kain yang harus terjual ?
c) jika A merupakan daerah asal ( domain ) fungsi f dan B merupakan daerah hasil (range) fungsi f , gambarkanlah permasalahan butir (a) dan butir (b) diatas.

Diket : x = banyak kain

           f(x) = 500x + 1000

Ditanya : a) nilai f(x), jika x = 50

               b) nilai x, jika f(x) = 100000

Jawab :

a) f(x) = 500x + 1000

    f(50) = 500(50) + 1000

            = 25000 + 1000

            = 26.000

Jadi, keuntungan yang didapat jika kain yang terjual sebanyak 50 adalah 26.000

b) f(x) = 500x + 1000

    100.000 = 500x + 1.000

     500x = 100.000 – 1.000

     500x = 99.000

     x = 99.000 ÷ 500

     x = 198

Jadi, jumlah kain yang terjual jika keuntungannya 100.000 adalah 198 kain.

2. Tentukanlah fungsi invers dari fungsi fungsi berikut jika ada
a. f(x) = 2x² + 5
b. g(x) = 2x – 1
———-
6
c. h(x) = ³√x+2

a) f(x) = 2x² + 5  

   f⁻¹(x) =

   f⁻¹(x) =

b) g(x) =

   g⁻¹(x) =

   g⁻¹(x) =

c) h(x) =

   h⁻¹(x) =

     h⁻¹(x) = x³ – 2

3. Diketahui f dan G suatu fungsi dengan rumus fungsi f(x) = 3x+4 dan g(x)=x-4/3 Buktikanlah bahwa f-¹=(gx) dan g-¹(x)=f(x)

F ⁻¹(x) = 3x+4
      y = 3x+4
3x+4 = y
   3x = y-4
     x = y-4 per 3
f ⁻¹(x) = x-4 per 3

g ⁻¹(x) = x-4 per 3
       y = x-4 per 3
     3y = x-4
  x-4  = 3y
     x = 3y+4

g ⁻¹(x) = 3x+4

4. Diketahui fungsi F:R->R dengan rumus fungsi F(x)=x²-4.tentukanlah daerah asal fungsi f agar fungsi f memiliki invers dan tentukan pula rumus fungsi inversnya untuk daerah asal yang memenuhi!

Daerah asal fungsi adalah semua bilangan riil.
Rumus fungsi inversnya adalah
x = y^2 – 4
X+4 = y^2
✓x+4 = y
✓x+4 = f(x)
Daerah asal fungsi inversnya adalah
✓x+4 ≥ 0
X+4 ≥ 0 (dikuadratkan)
X ≥ -4

5. Untuk mengubah satuan suhu dalam derajat celcius (°C) ke satuan suhu dalam derajat fahrenheit (°F) ditentukan dengan rumus F=9/5C+32.
a) Tentukan rumus untuk mengubh satun derajat fahrenheit (°F) ke satuan suhu dalam derajat Celcius (°C).
b) Jika seorang anak memiliki suhu badan 86°F, tentukanlah suhu badan anak itu jika diukur menggunakan satuan derajat Celcius!

A. C = (F – 32) 5/9

B. C = (86 – 32) 5/9
=54 * 5/9
=6*5
=30°C

6. Jika f-1 (x) = x -1/5 dan g-1 (x) = 3-x/2 dan, tentukanlah nilai (fog) -1(x)!

F⁻¹(x)= (x – 1)/5

g⁻¹(x)= (3-x)/2

(fog)⁻¹(x) = g⁻¹ ₀ f⁻¹ (x) = g⁻¹ {f⁻¹(x)} =

= g⁻¹ ((x-1)/5)) 

= { 3 – (x-1)/5)} / 2 …kalikan  5/5

= 5(3 – (x-1)/5))/ 5(2)

= (15 -(x-1)) / (10)

= 15 -x + 1 / (10)

= (16 -x)/(10)

7. Diketahui fungsi f: R-R dan g: R-R dirumuskan dengan f(x)= x-1/x, untuk x tidak sama dengan 0 dan g(x) = x+3. tentukanlah (gof)^-1(x)

8. Diketahui f(x) =3 (pangkat x-1) . Tentukan rumus fungsi f(pangkat -1) (x) dan tentukan juga f(pangkat -1)(81)

9. Diketahui fungsi f(x)= 2x + 3 dan (fog) (x + 1) = -2x²-4x-1, tentukanlah g-¹ (x) dan g-¹ (-2)

Fog(x+1) = -2x² – 4x – 1

fog(x) = -2(x-1)² -4(x-1) – 1

fog(x)= -2(x² -2x + 1) – 4x + 4 – 1

fog(x) = -2x² + 4x -2 – 4x + 3

fog(x) = -2x² + 1

f(x) = 2x+ 3

f⁻¹(x)= ¹/₂ (x – 3)

g(x)= f⁻¹ o fog

g(x)= ¹/₂ {-2x² +1-3) = – x² – 1

y = -x² – 1

x² = -y – 1

x = √(-y-1)

g⁻¹(x)= √(-x-1)

10. Fungsi f: R-R dan g: R-R ditentukan oleh rumus f(x) = x+2 dan g(x)=2x. tentukanlah rumus fungsi komposisi (fog)^-1(x) dan (gof)^-1(x)

Fog(x) = f(2x) = 2x+ 2

fog^-1(2x+2) = x

2x+2 = a

(x+1) = 1/2 a

x = 1/2 a – 1

(fog)^-1(a) = 1/2 a – 1

(fog)^-1(x) = 1/2 x – 1= (x-2)/2

.

gof (x) = g(x+2) = 2(x+2) = 2x+ 4

(gof)^-1 (2x+4) = x

2x + 4= a

2x = a-4

x = (a-4)2

(gof)^-1(a) = (a-4)/2

(gof)^-1(x) = (x-4)/2 

11. Diketahui f(x)=√x²+1 dan (fog)(x)=1/x-2√x²-4x+5 tentukan (fog)–1(x)

f(x) = √(x²+1)

f⁻¹(x) = √(x²-1)

(fog)(x) = (√(x²-4x+5))/(x-2)

             = √((x²-4x+5)/(x²-4x+4))

             = √((1/(x-2))² + 1)

             (fog)(x) = f(g(x))

√((1/(x-2))² + 1) = √(g(x))²+1)

                  g(x) = 1/(x-2)

                 g⁻¹(x) = (1+2x)/x

(fog)⁻¹(x) = g⁻¹(f⁻¹(x))

               = (1+2.(f⁻¹(x)))/(f⁻¹(x))

               = 2 + 1/(f⁻¹(x))

               = 2 + 1/√(x²-1)

12. Diketahui f(x) =x+1/x,x tidak sama dengan 0 dan f-¹ adalah invers dari f.jika k adalah banyaknya faktor prima dari 210 maka f-¹(k)=

F(x) = (x+1)/(x)
f⁻¹(x)= 1/(x-1)

k = (2,3,5,7)
n(k) = 4

f⁻¹(4) = 1/(4-1) = 1/3