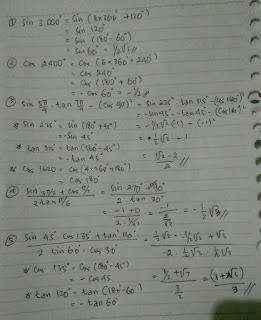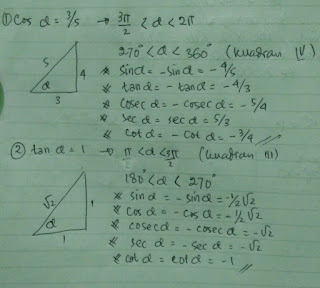Jawaban Buku Matematika Kelas 10 Uji Kompetensi 4.4 Kurikulum 2013
1. Tanda nilai perbandingan a berada di kuadran ke…..
a) sin a>0 | cos a>0
b) sin a<0 | cos a>0
c) tan a<0 | sin a>0
d) tan a=0 | sin a>0
e) csc a<0 | tan a<0
b) sin a<0 | cos a>0
c) tan a<0 | sin a>0
d) tan a=0 | sin a>0
e) csc a<0 | tan a<0
berikan alasan untuk setiap jawaban yang kamu peroleh…
Pembahasan :
a) sin a > 0 | cos a > 0
sin a bernilai positif jika a berada di kuadran I dan kuadran II
cos a bernilai positif jika a berada di kuadran I dan kuadran IV
karena sin a > 0 dan cos a > 0, maka a berada di kuadran I
b) sin a < 0 | cos a > 0
sin a bernilai negatif jika a berada di kuadran III dan kuadran IV
cos a bernilai positif jika a berada di kuadran I dan kuadran IV
karena sin a < 0 dan cos a > 0, maka a berada di kuadran IV
c) tan a < 0 | sin a > 0
tan a bernilai negatif jika a berada di kuadran II dan kuadran IV
sin a bernilai positif jika a berada di kuadran I dan kuadran II
karena tan a < 0 dan sin a > 0, maka a berada di kuadran II
d) tan a = 0 | sin a > 0
Kemungkinan disini ada kesalahan untuk tan a nya apakah tan a > 0 atau tan a < 0, karena jika tan a = 0 maka sin a juga pasti akan sama dengan 0. Kemungkinan terbesar adalah tan a > 0 karena tan a < 0 sudah ditanyakan di bagian c
Jadi soal seharusnya adalah: tan a > 0 | sin a > 0
tan a bernilai positif jika a berada di kuadran Idan kuadran III
sin a bernilai positif jika a berada di kuadran I dan kuadran II
karena tan a > 0 dan sin a > 0, maka a berada di kuadran I
e) cosec a < 0 | tan a < 0
Jawab
cosec a bernilai negatif jika a berada di kuadran III dan kuadran IV
tan a bernilai negatif jika a berada di kuadran II dan kuadran IV
karena cosec a < 0 dan tan a < 0, maka a berada di kuadran IV
2. Hitung nilai dari :
a. sin 3.000°
b. cos 2.400°
c. sin 5π/4×tan 7π/4-(cos 9π)²
d. sin 3π/2+cos π/2 per 2tan π/6
e. sin 45°×cos 135°+tan²120° per 2 sin 60°×cos 30°°
a. sin 3.000°
b. cos 2.400°
c. sin 5π/4×tan 7π/4-(cos 9π)²
d. sin 3π/2+cos π/2 per 2tan π/6
e. sin 45°×cos 135°+tan²120° per 2 sin 60°×cos 30°°
Pembahasan :
3. Tentukan lima nilai perbandingan trigonometri yang lain untuk setiap pernyataan berikut ini.
a. cos alfa = 3/5 , 3π/2<alfa<2π
b. tan alfa = 1 , π<alfa<πc. 4 Sin a = 2 , π/2 <alfa<π
d. sec betha = -2 , π < betha < 3π/2
e. csc betha = -2√3/2 , 3π/2 < betha < 2π
f. 3 tan ^2 betha = 1 , π/2 < betha < π
a. cos alfa = 3/5 , 3π/2<alfa<2π
b. tan alfa = 1 , π<alfa<πc. 4 Sin a = 2 , π/2 <alfa<π
d. sec betha = -2 , π < betha < 3π/2
e. csc betha = -2√3/2 , 3π/2 < betha < 2π
f. 3 tan ^2 betha = 1 , π/2 < betha < π
Pembahasan :
4. Selidiki kebenaran setiap pernyataan berikut. Berikan alasan untuk setiap jawabanmu.
a. Sec x dan sin x selalu memiliki nilai tanda yang sama di keempat kuadrat.
b. Di kuadran I, nilai sinus selalu lebih besar daripada nilai cosinus.
c. Untuk 30 derajat < x < 90 derajat, dan 120 derajat < y < 150 derajat, maka nilai 2, sin x < cos 2y
a. Sec x dan sin x selalu memiliki nilai tanda yang sama di keempat kuadrat.
b. Di kuadran I, nilai sinus selalu lebih besar daripada nilai cosinus.
c. Untuk 30 derajat < x < 90 derajat, dan 120 derajat < y < 150 derajat, maka nilai 2, sin x < cos 2y
Pembahasan :
A. Tidak
alasan : sec x = 1/ cos x bandingkan dgn sin x
kw I : 1/cos x = +
sin x = +
kw II : 1/cos x = –
sin x = +
(lihat kw II tdk sama tanda, cukup untuk mewakili alasan)
b. Tidak
Alasan : Kw I : sin 30 = 1/2 =0,5
cos 30 = 1/2√3 = 0,86..
Sin 30 < cos 30
(cukup untuk mewakili alasan)
3. Tidak
Alasan :
2 sin x –> misal x = 45
2 sin 45 = 2. 1/2√2 = √2 = 1,414
cos 2y –> misal y = 135
cos 2y = 1- 2 sin²y
= 1 – 2. sin²135
= 1 – 2. sin²45
= 1 – 2. (1/2√2)²
= 1 – 2. 1/4. 2
= 1-1
= 0
sehingga
1,414 < 0 (tidak)
cukup mewakili alasan
5. Diberikan tan theta = -8/15 dengan sin theta > dengan 0 tentukan.
a. cos theta
b. csc theta
c.sin theta × cos theta + cos theta × sin theta
d. csc theta/cot theta
a. cos theta
b. csc theta
c.sin theta × cos theta + cos theta × sin theta
d. csc theta/cot theta
Pembahasan :
6. Dengan menggunakan identitas trigonometri, sederhanakan setiap bentuk berikut ini :
a) (tan x + sec x) (tan x – sec x)
b) 1 / (1 + cos x) + 1 / (1 – cos x)
c) tan x – sec² x / tan x
d) (cos x) / (1+ sin x) + (1+sin x) / (cos x)
a) (tan x + sec x) (tan x – sec x)
b) 1 / (1 + cos x) + 1 / (1 – cos x)
c) tan x – sec² x / tan x
d) (cos x) / (1+ sin x) + (1+sin x) / (cos x)
Pembahasan :
7. Diketahui Alfa(a)=45° dan Beta(b)= 60°,Hitung!
1. 2 × sin 45° × cos 60°
2. sin 45° × cos 60° + sin 60° ×
cos 45 °
3. sin 45° × cos 60° – sin 60° × cos 45°
4. tan 45° + tan 60° /1(tan 45° × tan 60°)
5. sin²45° + cos²60° +sin²60° + cos²45°
1. 2 × sin 45° × cos 60°
2. sin 45° × cos 60° + sin 60° ×
cos 45 °
3. sin 45° × cos 60° – sin 60° × cos 45°
4. tan 45° + tan 60° /1(tan 45° × tan 60°)
5. sin²45° + cos²60° +sin²60° + cos²45°
Pembahasan :
8. Diberikan fungsi f(x) = sin (x + 90°) , untuk setiap 0° < x < 360° untuk semua sudut sudut istimewa , tentukan nilai fungsi
Pembahasan :
9. Sederhanakan bentuk persamaan berikut ini.
a. cos x . csc x. tan x.
b. cos x cot c + sin x
c. sin x / 1+ cos x + sin x / 1 – cos x
d. (sin x + cos x )² + ( sin x – cos x )²
e.( csc theta – cot theta) × ( sin x – cos x)²
tolong dijwab dengan langkah langkah.x
a. cos x . csc x. tan x.
b. cos x cot c + sin x
c. sin x / 1+ cos x + sin x / 1 – cos x
d. (sin x + cos x )² + ( sin x – cos x )²
e.( csc theta – cot theta) × ( sin x – cos x)²
tolong dijwab dengan langkah langkah.x
Pembahasan :
10. Cermati gambar 4.35. dengan menemukan hubungan antar sudut dan panjang sisi pada segitiga siku siku yg ada pada gambar, hitung:
a. panjang AD, EC, BC, BD, AB, FB, AE, dan DE
b. sin 75′
c. cos 75′
d. tan 75′
a. panjang AD, EC, BC, BD, AB, FB, AE, dan DE
b. sin 75′
c. cos 75′
d. tan 75′
Pembahasan :