SOAL DAN PEMBAHASAN BUKU SISWA MATEMATIKA KLS 8 SEMESTER 2
UJI KOMPETENSI 7 HALAMAN 113
1. Diketahui suatu juring lingkaran dengan ukuran sudut pusat 90° jika luas juring tersebut
adalah78,5 cm², maka jari-jari lingkaran tersebut adalah….(π=3,14)
Pembahasan :
Luas juring = (α/ 360°) π r²
78,5 = (90°/360°) x 3,14 x r²
78,5 = 0,785 x r²
r² = 78,5 / 0,785
= (78,5 X 1000) / (0,785 X 1000)
= 78500/785
= 100
r = 10
Jadi jari-jari lingkaran tersebut adalah 10 cm
2. Diketahui panjang busur suatu lingkaran adalah 22 cm. Jika sudut pusat yg menghadap
busur tersebut berukuran 1200, maka panjang jari jari juring lingkaran tersebut
adalah….cm (π = 22/7)
Pembahasan:
Panjang busur suatu lingkaran adalah 22 cm dan π = 22/7
Keliling lingkaran = 2. π.r
120°/360° x 2.π.r = 22 cm
1/3 x 2 x 22/7 x r = 22 cm
44/21 . r = 22 cm
r = 21/44 x 22 cm
r = 21/2
r = 10,5 cm
Jadi panjang jari jari juring lingkaran tersebut adalah 10,5 cm
3. Diketahui panjang busur suatu lingkaran adalah 16,5 cm. Jika panjang diameter
lingkaran tersebut adalah 42 cm, maka ukuran sudut pusatnya adalah ….(π = 22/7)
Pembahasan :
Dik: Panjang busur = 16,5 cm dan d = 42 cm dan π = 22/7
Dit: a = …o
Jawab:
a/360° . π . d = 16,5
a/360° . 22/7 . 42 = 16,5
a = 16,5 . (7 . 360°) / (22 . 42)
a = 45°
4. Diketahui suatu juring lingkaran memiliki luas 57,75 cm2. Jika besar sudut pusat
yang bersesuaian dengan juring tersebut adalah 60°, maka panjang jari jari
lingkaran tersebut adalah….( π = 22/7)
Pembahasan :
Dik: L.juring = 57,75 dan a = 60o dan π = 22/7.
Dit: r = …
Jawab: L.juring = a/360o x π×r²
Luas juring = 60/360 × π × r²
57,75 = 1/6 × 22/7 × r²
57,75 = 0,523 × r²
r² = 57,75 / 0,523
= (57,75 x 1000) / (0,523 x 1000)
= 57750/523
r² = 110,25
r = √110,25 = 10,5 cm
Jawabannya adalah yang b. 10,5 cm
5. Panjang busur lingkaran dengan jari jari 21 cm dan sudut pusat 30° adalah…( π = 22/7).
Pembahasan :
Dik: r = 21 cm dan sudut pusat (a) = 30° dan π = 22/7
Dit: Panjang busur = …
Jawab:
Panjang busur = sudut pusat/360° × K. lingkaran
= 30°/360° × (2 × π × r)
= 1/12 × (2 × 22/7 × 21)
= 1/12 × 132
= 11 cm (A)
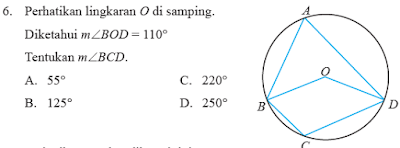
Pembahasan :
Menghitung besar ∠BAD, yaitu:
∠BAD =1/2 ∠BOD (besar <pusat = 1/2 < keliling)
∠BAD = 1/2 x 110°
∠BAD = 55°
Menghitung besar ∠BCD, yaitu:
∠BAD + ∠BCD = 180° (jumlah < yang berhadapan)
∠BCD = 180° – ∠BAD
∠BCD = 180° – 55° = 125°
Maka dapat diketahui besar m∠BCD = 125°
Pembahasan :
Tidak ada jawaban dipilihan gandanya kalau menurut saya.
3AQB = 144
AQB = 144/3
AQB = 48
Sudut pusat = 2 x Sudut keliling
AOB = 2 x AQB
AOB = 2 x 48
AOB = 96°
8. Suatu ban mobil berdiameter 60 cm (0,6m). Ban tersebut bergaransi hingga
menempuh 10.000km. Sampai dengan berapa putaran ban tersebut hingga masa
garansinya habis? (1 km=1000m).
Pembahasan :
Panjang lintasan = n x keliling lingkaran
Panjang lintasan = n x π x d
10.000 km = n x 3,14 x 60 cm
10.000 km = n x 188,4 cm
1.000.000.000 cm = n x 188,4 cm
n = 1.000.000.000 cm / 188,4 cm
n = 5.307.855,63 = 5.307.856
Jadi, ban berputar sebanyak 5.307.856 kali hingga masa garansinya habis.
Pembahasan :
Keliling lingkaran = 2πr
Perhatikan gambar, keliling daerah tertutup bagian yang diarsir biru
= 1/4 keliling lingkaran +26 cm +26 cm +1/4 keliling lingkaran +26 cm + 26 cm
= 1/2 keliling lingkaran + (4 × 26cm)
= (1/2)(2πr) + 104 cm = πr + 104cm
= (22/7)(14cm) + 104 cm = 44 cm + 104 cm = 148 cm
Jadi, keliling bagian yang diarsir biru adalah 148 cm.
Pembahasan :
Dik: Luas persegi = S × S = 14 × 14 = 196 cm2
Dit : luas daerah yg diarsir
Jawab :
Luas 1/2 Lingkaran = 1/2Πr2
= ½ × 22/7 × 72
= 77 cm2
Jadi luas daerah yg diarsir adalah = 196 + 77 = 273 cm2
11. Diketahui panjang garis singgung persekutuan luar lingkaran C dan D
adalah 12 cm. Jari jari lingkaran C dan D berturut-turut 7.5 cm dan 4 cm.
Jarak antara kedua pusat lingkaran tersebut adalah… Cm
Pembahasan :
Menentukan jarak kedua pusat adalah:
p² = j² + (R – r)²
p² = (12 cm)² + (7.5 cm – 4 cm)²
p² = 144 cm² + 12.25 cm²
p² = 156.25
p = √156.25
p = 12.5 cm
12. Diketahui jarak antara pusat lingkaran A dan B adalah 7,5 cm. Lingkaran A
dan B memiliki jari-jari berturut-turut 2,5 cm dan 2 cm. Panjang garis singgung
persekutuan dalam kedua lingkaran tersebut adalah
Pembahasan :
Panjang garis singgung = √(jarak pusat² – (R + r)²)
= √(7,5² – (2,5 + 2)²)
= √(56,25 – 20,25)
= √36
= 6 cm
13. Diketahui dua lingkaran dengan ukuran jari jari lingkaran pertama lebih dari
lingkaran kedua. Jari jari lingkaran pertama adalah 1,5 cm. Sedangkan jarak
pusat kedua lingkaran tersebut adalah 2,5 cm. Jika panjang garis singgung
persekutuan luar kedua lingakaran tersebut adalah 2,4 cm. Maka diameter adalah…cm.
Pembahasan :
d² = p² – (R – r)²
2,4² = 2,5² – (1,5 – r)²
5,76 = 6,25 – (1,5 – r)²
(1,5 – r)² = 6,25 – 5,76
(1,5 – r)² = 0,49
1,5 – r = √0,49
1,5 – r = 0,7
r = 1,5 – 0,7 = 0,8 cm
jari-jari lingkaran kedua = 0,8 cm
diameter = 2r = 2 × 0,8 cm = 1,6 cm